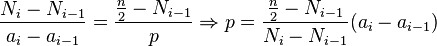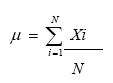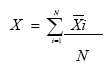Medidas de Tendencia Central y de Variabilidad Contenidos
Medidas de tendencia central: media, mediana y moda
Medidas de dispersión: rango,varianza y desviación estándar.
MEDIDAS DE TENDENCIA CENTRAL: Moda, mediana y
media
Tendencia central : La tendencia central se refiere al punto medio de
una distribución.
Las medidas de tendencia central se denominan medidas de
posición.
La Moda: En una serie de puntuaciones se denomina moda a la
observación que se presenta con mayor frecuencia.
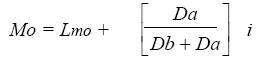
Mo = Moda
Lmo = Límite inferior del intervalo de clase modal
Da = Diferencia entre la frecuencia de la clase modal y la de la clase que la precede.
Db = Diferencia entre la frecuencia de la clase modal y la de la clase que l la sigue.
i = Intervalo de clase.
La moda para una distribución de frecuencias agrupadas se obtiene a partir de los datos de la Tabla 4.2:
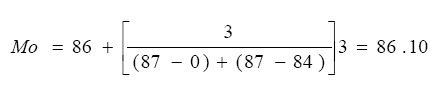
la moda tiene un valor de 86.10.
Ejemplo 1: Los siguientes datos representan la cantidad de pedidos diarios
recibidos en un período de 20 días, ordenados en orden ascendente
0 0 1 1 2 2 4 4 5 5 6 6 7 7 8 12 15 15 15 19
Mo = 15 La cantidad de pedidos diarios que más se repite es 15
Ejemplo 2: La cantidad de errores de facturación por día en un período de 20 días,
ordenados en orden ascendente es
0 0 1 1 1 2 4 4 4 5
6 6 7 8 8 9 9 10 12 12
Esta distribución tiene 2 modas. Se la llama distribución bimodal .
Mo = 1 y Mo = 4
Calcular la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
Mo = 5
Calcular la moda.
Mo = 12
.Calcular la moda de una distribución estadística que viene dada
por la siguiente tabla:

.Calcular la moda de una distribución estadística viene dada por
la siguiente tabla:
.Calcular la moda de la distribución estadística:
.El histograma de la distribución correspondiente al peso de
100 alumnos de Bachillerato es el siguiente:

Calcular la moda.
.En la siguiente tabla se muestra las calificaciones (suspenso,
aprobado, notable y sobresaliente) obtenidas por un grupo de 50
alumnos. Calcular la moda.
Cálculo de la moda para datos agrupados
Si los datos están agrupados en una distribución de frecuencias, se selecciona
el intervalo de clase
que tiene mayor frecuencia llamado clase modal.
Para determinar un solo valor de este intervalo para la moda utilizamos la siguiente
ecuación:

La Mediana:
También conocida como media posicional en virtud de que se localiza en el centro de un conjunto de observaciones presentadas en una serie ordenada de datos. Lo anterior sugiere que el 50 % de los casos se encuentra por encima de la mediana y el resto por debajo de ella. La posición central de la mediana se obtiene mediante la expresión matemática.
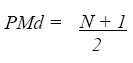
(Ec. 4.4)
donde:
PMd = Posición de la Mediana
N = Número de casos.
el procedimiento para obtener la mediana a partir de una distribución de frecuencias simple o agrupada requiere de aplicar la expresión:
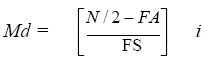
(Ec. 4.5)
donde:
Md = Mediana
N = Número de casos.
FA = Frecuencia agrupada.
FS = Frecuencia del intervalo adyacente superior.
Al aplicar la ecuación 4.5 a los datos de la Tabla 4.2 se obtiene un valor de 83 para la mediana:
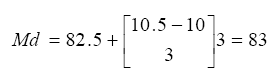
Ejemplo: tenemos el siguiente conjunto de números 8,3,7,4,11,2,9,4,10,11,4 ordenamos: 2,3,4,4,4,7,8,9,10,11,11 En esta secuencia la mediana es 7, que es el número central.
Y si tuviésemos: 8,3,7,4,11,9,4,10,11,4,
entonces ordenamos: 3,4,4,4,7,8,9,10,11,11 y la mediana (Md) está en: los números
centrales son 7 y 8, lo que haces es sumar 7 + 8
y divides entre 2 y Md= 7.5.
Existen dos métodos para el cálculo de la mediana:
- Utilizando los datos agrupados en intervalos de clase.Sean
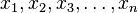 los datos de una muestra ordenada en orden crecientey designando la mediana como
los datos de una muestra ordenada en orden crecientey designando la mediana como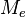 , distinguimos dos casos:a) Si n es impar, la mediana es el valor que ocupa la posición
, distinguimos dos casos:a) Si n es impar, la mediana es el valor que ocupa la posición una vez quelos datos han sido ordenados (en orden creciente o decreciente), porque éste esel valor central.Es decir:
una vez quelos datos han sido ordenados (en orden creciente o decreciente), porque éste esel valor central.Es decir: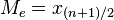 .Por ejemplo, si tenemos 5 datos, que ordenados son:
.Por ejemplo, si tenemos 5 datos, que ordenados son: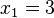 ,
, 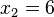 ,
, 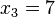 ,
, 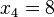 ,
, 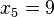 => El valor central es el tercero:
=> El valor central es el tercero: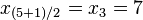 . Este valor, que es la mediana deese conjuntode datos, deja dos datos por debajo (
. Este valor, que es la mediana deese conjuntode datos, deja dos datos por debajo ( ,
,  ) y otros dos por encima de él (
) y otros dos por encima de él ( ,
,  ).b) Si n es par, la mediana es la media aritmética de los dos valores centrales.Cuando
).b) Si n es par, la mediana es la media aritmética de los dos valores centrales.Cuando es par, los dos datos que están en el centro de la muestra ocupan las posiciones
es par, los dos datos que están en el centro de la muestra ocupan las posiciones y
y 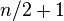 . Es decir:
. Es decir: 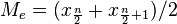 .Por ejemplo, si tenemos 6 datos, que ordenados son:
.Por ejemplo, si tenemos 6 datos, que ordenados son: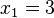 ,
, 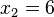 ,
, 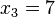 ,
, 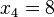 ,
, 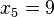 ,
, 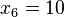 => Hay dos valoresque están por debajo del
=> Hay dos valoresque están por debajo del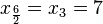 y otros dos que quedan por encima del siguiente dato
y otros dos que quedan por encima del siguiente dato . Por tanto, la mediana de este grupo de datoses la media aritmética de estos dos datos:
. Por tanto, la mediana de este grupo de datoses la media aritmética de estos dos datos: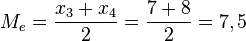 .Al tratar con datos agrupados, si
.Al tratar con datos agrupados, si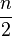 coincide con el valor de una frecuenciaacumulada, el valor de la mediana coincidirá con la abscisa correspondiente.Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanzade triángulos en el histograma o polígono de frecuencias acumuladas, utilizandola siguiente equivalencia:Donde
coincide con el valor de una frecuenciaacumulada, el valor de la mediana coincidirá con la abscisa correspondiente.Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanzade triángulos en el histograma o polígono de frecuencias acumuladas, utilizandola siguiente equivalencia:Donde y
y 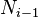 son las frecuencias absolutas acumuladas tales que
son las frecuencias absolutas acumuladas tales que ,
, 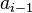 y
y  son los extremos, interior y exterior, del intervalo donde se alcanza la mediana y
son los extremos, interior y exterior, del intervalo donde se alcanza la mediana y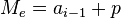 es la abscisa acalcular, la mediana. Se observa que
es la abscisa acalcular, la mediana. Se observa que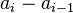 es la amplitud de los intervalos seleccionados para el diagrama.ejemplos:1. Hallar la mediana de la siguientes series de números:3, 5, 2, 6, 5, 9, 5, 2, 8.2, 2, 3, 5, 5, 5, 6, 8, 9.Me = 53, 5, 2, 6, 5, 9, 5, 2, 8, 6.2, 2, 3, 5, 5, 5, 6, 6, 8, 9.10/2 = 5
es la amplitud de los intervalos seleccionados para el diagrama.ejemplos:1. Hallar la mediana de la siguientes series de números:3, 5, 2, 6, 5, 9, 5, 2, 8.2, 2, 3, 5, 5, 5, 6, 8, 9.Me = 53, 5, 2, 6, 5, 9, 5, 2, 8, 6.2, 2, 3, 5, 5, 5, 6, 6, 8, 9.10/2 = 5 10, 13, 4, 7, 8, 11 10, 16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 183, 4, 4, 5, 6, 7, 7, 8, 8, 9, 9, 10, 10, 10, 10, 11, 12, 13, 13, 14, 16, 16, 17, 18, 18, 20
10, 13, 4, 7, 8, 11 10, 16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 183, 4, 4, 5, 6, 7, 7, 8, 8, 9, 9, 10, 10, 10, 10, 11, 12, 13, 13, 14, 16, 16, 17, 18, 18, 20 2. Tabular y calcular mediana de la siguiente serie de números: 5, 3, 6, 5, 4,5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
2. Tabular y calcular mediana de la siguiente serie de números: 5, 3, 6, 5, 4,5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
- 20/2 = 10 Me = 53. Hallar la mediana de la distribución estadística que viene dada por la siguiente tabla:
 4. Calcular la mediana de las alturas de los jugadores de un equipo de baloncesto,que vienen dadas por la tabla:
4. Calcular la mediana de las alturas de los jugadores de un equipo de baloncesto,que vienen dadas por la tabla:
 ara calcular la mediana, ordena los números que te han dado según su valor
ara calcular la mediana, ordena los números que te han dado según su valor
Mira estos números:3, 13, 7, 5, 21, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29Si los ordenamos queda:3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56Hay quince números. El del medio es el octavo número:3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56La mediana de este conjunto de valores es 23.
Cálculo de la mediana para datos agrupados:
Si los datos están agrupados en una distribución de frecuencias, se selecciona el intervalo
de
clase que contiene a la mediana llamado clase mediana. Para ello, debemos determinar
la frecuencia
acumulada absoluta que contenga al elemento número n + 1/2
. El valor de este intervalo para la
mediana se calcula utilizando la siguiente ecuación:

Media Aritmética: Medida de tendencia central que se define como el promedio o media de un conjunto de observaciones o puntuaciones. En aquellas situaciones en que la población de estudio es pequeña suele utilizarse la media poblacional mediante la expresión:
(Ec. 4.1)donde:µ = media poblacionalΣXi = Sumatoria de las puntuacionesN = Número de casos
En cambio si la población de estudio es muy numerosa se procede a obtener la media muestral definida matemáticamente por la expresión:
(Ec. 4.2)donde:X = media muestralΣXi = Sumatoria de las puntuacionesN = Número de casos
Al obtener la media alcanzada por la compañía XYZ que comercializa computadoras personales. Las ventas diarias realizadas por la compañía durante una semana indican las siguientes cantidades: 4, 12, 7, 9, 11, 7, 8, el cálculo de la media es:
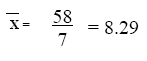
el anterior resultado sugiere que el promedio semanal de ventas de la compañía XYZ es de 8.29 computadoras personales.
ejemplos:
1.Considérense los siguientes datos: 3, 8, 4, 10, 6, 2. Se pide:
1. Calcular su media.
2. Si los todos los datos anteriores los multiplicamos por 3, cúal será la nueva media.
2. A un conjunto de 5 números cuya media es 7.31 se le añaden los números 4.47 y 10.15.
¿Cuál es la media del nuevo conjunto de números?
3.Calcular la media de una distribución estadística que viene dada por la siguiente
tabla:
4. Hallar la media de la distribución estadística que viene dada por la siguiente tabla:
5. Calcular la media de la distribución estadística:
6. Los resultados al lanzar un dado 200 veces vienen dados por la siguiente tabla:
Determinar a y b sabiendo que la puntuación media es 3.6.
a = 29 b = 36
Cálculo de la media para datos no agrupados :
Para calcular la media para datos agrupados, primero calculamos el punto medio de cada clase
(marca de clase mi
Después multiplicamos cada punto medio por la frecuencia absoluta de cada
intervalo

Medidas de Dispersión.
Las medidas de dispersión son índices que se utilizan para describir una distribución de frecuencias a partir de la variación de los valores obtenidos. Los índices más utilizados son el rango, la varianza y la desviación estándar.
El Rango:
Indice conocido como recorrido. Se le define como la diferencia existente entre la puntuación mayor y la menor en una serie de datos. Tiene como desventaja que solo toma en cuenta para su cálculo las puntuaciones extremas, es decir la mayor y la menor omitiendo el resto de los datos u observaciones. Debido a lo anterior no es una medida confiable dado que se obtiene prácticamente por inspección.
La Varianza:
La varianza es una medida de variabilidad que toma en cuenta el 100 % de las puntuaciones de manera individual. Webster (1998) la define como “la media aritmética de las desviaciones respecto a la media aritmética elevada al cuadrado,” (p. 83). La definición matemática de la varianza se expresa por medio de la ecuación 4.6:
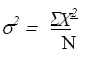
(Ec. 4.6)
donde:
σ2 = Varianza.
Σ = Suma de
X2= Desviación de las puntuaciones de la media (X-X)
N = Número de casos.
La Desviación Estándar:
Dada la dificultad inherente de interpretar el significado de una varianza en virtud de que expresa valores elevados al cuadrado, para efectos de investigación es más adecuado utilizar la desviación estándar o desviación típica, definida como la raíz cuadrada de la varianza. La desviación estándar se expresa mediante la ecuación 4.7:
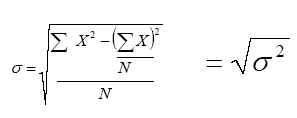
(Ec. 4.7)
donde:
Σ X2= Suma de los cuadrados de cada puntuación
(ΣX)2 = Suma de las puntuaciones elevadas al cuadrado
N = Número de casos.
σ = Desviación Estándar
BLOQUE 4:
ANALISIS DE DATOS EN DOS VARIABLES
CORRELACION Y REGRESION LINEAL
CORRELACION:
El análisis de correlación es un grupo de técnicas estadísticas usadas para medir la fuerza de la asociación entre dos variables. Un diagrama de dispersión es una gráfica que representa la relación entre dos variables. La variable dependiente es la variable que se predice o calcula. La variable independiente proporciona las bases para el cálculo. Es la variable de predicción.
El coeficiente de correlación:
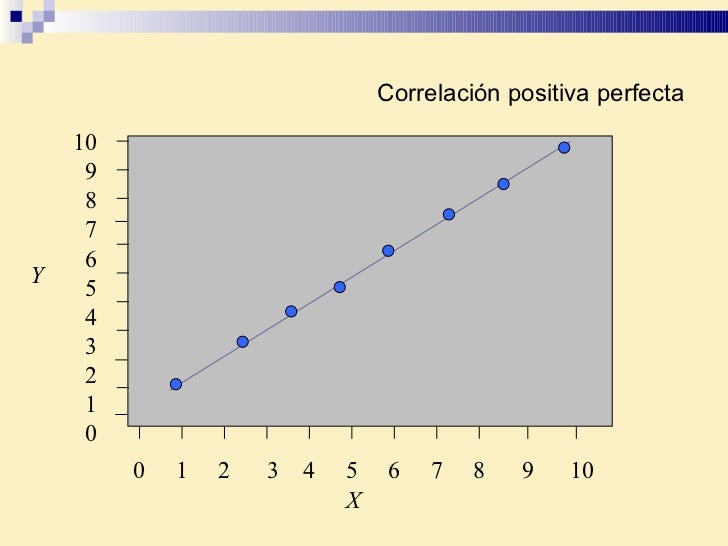
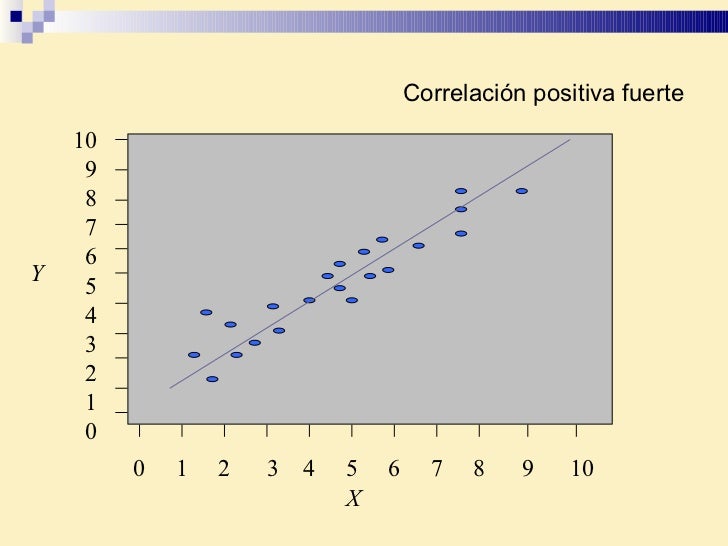
r El coeficiente de correlación ( r ) es una medida de la intensidad de la relación lineal entre dos variables. Requiere datos de nivel de razón. Puede tomar cualquier valor de -1.00 a 1.00. Los valores de -1.00 o 1.00 indican la correlación perfecta y fuerte. Los valores cerca de 0.0 indican la correlación débil. Los valores negativos indican una relación inversa y los valores positivos
indican una relación directa.
Correlación negativa perfecta
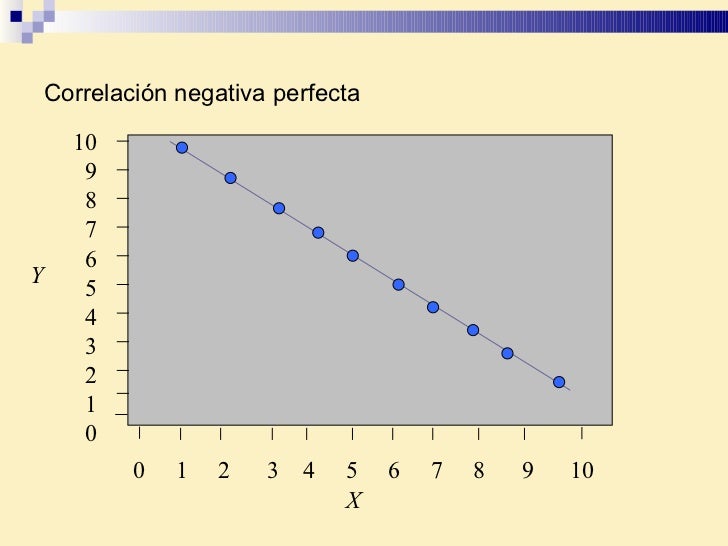
Correlación negativa perfecta 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 X Y
Correlación cero 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Y X
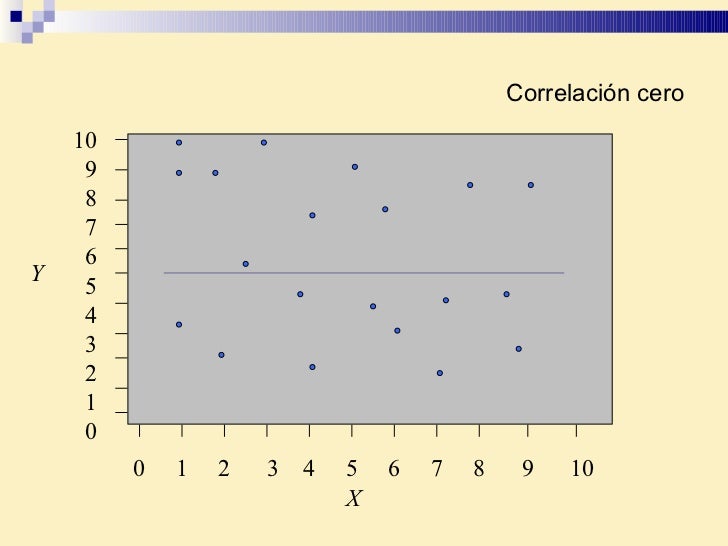
Correlación cero 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 Y X

- Coeficiente de determinación:
- El coeficiente de determinación ( r 2 ) es la proporción de la variación total en la variable dependiente ( y ) que se explica por la variación en la variable independiente ( x ) . Es el cuadrado del coeficiente de correlación. Su rango es de 0 a 1. No da ninguna información sobre la dirección de la relación entre las variables.
- Ejemplo 1:
- Juan Escobedo, presidente de la sociedad de alumnos de la Universidad de Toledo, se ocupa de estudiar el costo de los libros de texto. Él cree que hay una relación entre el número de páginas en el texto y el precio de venta del libro. Para proporcionar una prueba, selecciona una muestra de ocho libros de texto actualmente en venta en la librería. Dibuje un diagrama de dispersión. Compruebe el coeficiente de correlación.
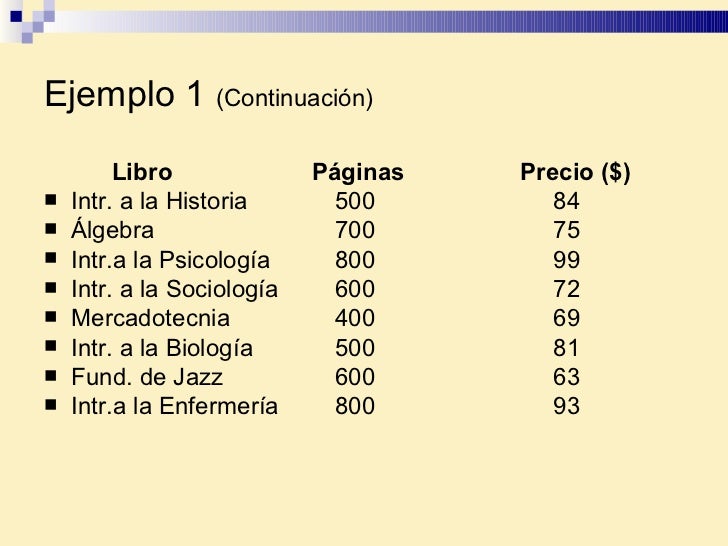
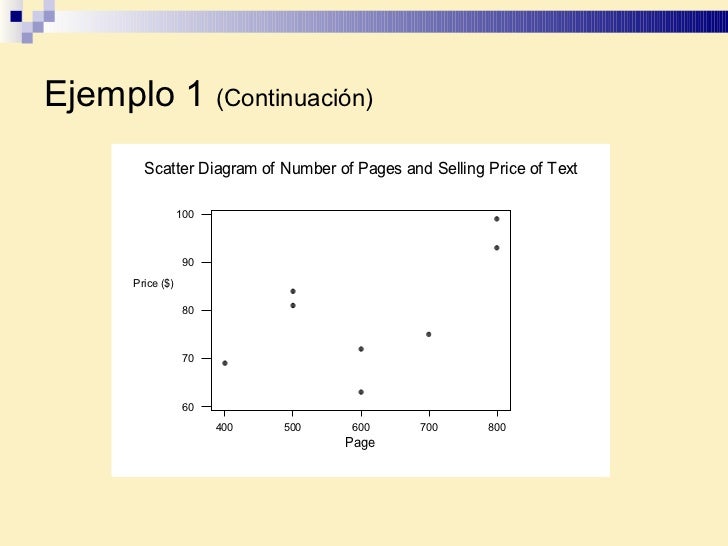
La correlación entre el número de páginas y el precio de venta del libro es 0.614. Esto indica una asociación moderada entre las variables. Pruebe la hipótesis de que no hay correlación en la población. Utilice un nivel de la significancia del .02. Paso 1: H 0 : La correlación en la población es cero. H 1 : La correlación en la población no es cero. Paso 2: H 0 es rechazada si t >3.143 o si t <-3.143 . Hay 6 grados de libertad, encontrados cerca. n – 2 = 8 – 2 = 6.
Para encontrar el valor del estadístico de prueba, utilizamos: Paso 4: H 0 no se rechaza. No podemos rechazar la hipótesis de que no hay correlación en la población. La cantidad de asociación puede ser debido al azar.
Análisis de regresión:
En análisis de regresión utilizamos la variable independiente ( X ) para estimar la variable dependiente ( Y ) . La relación entre las variables es lineal. Ambas variables deben ser por lo menos escala del intervalo. El criterio de mínimos cuadrados se utiliza para determinar la ecuación. Este es el término (Y – Y') 2
La ecuación de regresión es: Y' = a + bX, donde: Y' es el valor pronosticado de la variable Y para un valor seleccionado de X . a es la ordenada de la intersección con el eje Y cuando X = 0. Es el valor estimado de Y cuando X= 0 b es la pendiente de la recta, o el cambio promedio en Y' para cada cambio de una unidad en X. el principio de mínimos cuadrados se utiliza para obtener a y b El principio de mínimos cuadrados se utiliza para obtener a y b . Las ecuaciones para determinar a y b son:
- Desarrolle una ecuación de regresión para la información dada en el Ejemplo 1 que se puede utilizar para estimar el precio de venta basado en el número de páginas. Ejemplo 2 (Continuación)
- . La ecuación de regresión es: Y' = 48.0 + .05143X La ecuación cruza al eje Y en $48. Un libro sin las páginas costaría $48. La pendiente de la línea es .05143. El costo de cada página adicional es de cinco céntimos. El signo del valor de b y el signo del valor de r serán siempre iguales. Ejemplo 2 (Continuación)
- Podemos utilizar la ecuación de regresión para estimar valores de Y. El precio de venta estimado de un libro de 800 páginas es $89.14, encontrado por Ejemplo 2 (Continuación)
- El error estándar de estimación :
- El error estándar de estimación mide la dispersión de los valores observados alrededor de la línea de regresión. Las fórmulas que se utilizan para comprobar el error estándar son:
- Suposiciones subyacentes en el análisis de regresión lineal Para cada valor de X, hay un grupo de valores de Y, y estos valores de Y se distribuyen normalmente. Las medias de estas distribuciones normales de valores Y, caen todas en la recta de regresión. Las desviaciones estándar de estas distribuciones normales son iguales. Los valores de Y son estadísticamente independendientes. Esto significa que en la selección de una muestra, los valores de Y elegidos para un valor particular de X no dependen de los valores de Y de ningún otro valor de X.
- Intervalo de confianza;
- El intervalo de confianza para el valor medio de Y para un valor dado de X está dado por:

- Intervalo de predicción:El intervalo de predicción para un valor individual de Y para un valor dado de X se da por:

- . Resumir los resultados: El precio de venta estimado para un libro con 800 páginas es $89.14. El error estándar de estimación es $10.41. El intervalo de confianza de 95% para todos los libros con 800 páginas es $89.14+-$15.31. Esto significa que los límites están entre $73.83 y $104.45. El intervalo de predicción de 95% para un libro particular con 800 páginas es $89.14+-$29.72. Esto significa que los límites están entre $59.42 y $118.86. Estos resultados aparecen en la siguiente salida de MINITAB.
- Coeficiente de correlación linealPara calcular el coeficiente de correlación lineal, se recomienda elaborar la siguiente tabla.Las columnas: casas, m2 de construcción y precio son las que fueron proporcionadas en los datos.La columna X^2 se obtiene elevando al cuadrado la variable "M2 de Construcción" (definida como "X" anteriormente). Ejemplo: 170*170 = 28,900La columna Y^2 se obtiene elevando al cuadrado la variable "Precio" (definida como "Y" anteriormente).Ejemplo: 850*850= 722,500La columna XY se obtiene multiplicando X*Y.Ejemplo: (170)(850)=144,500.